Dandelin Spheres

Ellipse

Ellipses are mysterious.
Unlike harmonious circles, they become incredibly complex with just a slight twist.

In high school, I suddenly became curious about the perimeter of an ellipse.

The area of an ellipse can be easily derived as abπ using definite integrals or orthogonal projection, but the perimeter was rarely mentioned, and the chapter wasn’t very deep.
It was probably only briefly mentioned later in the arc length section of integrals, around the ellipse and hyperbola part in the polar coordinates chapter.

It was enough to stimulate my curiosity at the time, and since I was fascinated by the charm of orthogonal projection, I attempted to find the perimeter of an ellipse using projection.

Questions

During my high school years, when I was prone to various delusions, I would post questions to Facebook math groups or bother teachers with emails to resolve these thoughts.
My dreams kept changing, but at the time (probably around my sophomore year), I was dreaming of majoring in mathematics. Various delusions diverged, but looking back, I don’t think I had the ability or will to converge them. Would it have been different if there had been a GPT to answer infinite questions? Sometimes, only regrets for what couldn’t be completed remain.

On Euler Day 2014, derived from Euler’s constant 2.7… on February 7th, I went to attend a public lecture about Euler at the Korea Institute for Advanced Study. I used to write on a Naver blog at the time, so I thought I had left some record somewhere, but now there’s no trace.
It feels like a lost memory, which is a bit regrettable. One of the reasons I write this blog now is because I don’t want to lose the things I wanted to remember. I was quite lazy even then, so what remains is probably this much. The dream of becoming a physicist didn’t last very long either.

Anyway, returning to Euler Day. I don’t remember exactly what lecture I attended, but it was probably a session about the beauty of Euler’s identity. Although it’s now forgotten, I was deeply impressed by the lecture and began to imagine. At the time, I was learning about complex numbers, geometry, and vectors, so I used to expand my imagination within the boundaries of learning. \

Quaternions

It wasn’t a purposeful thought experiment that would lead to something derived, but questions like ‘wouldn’t it be like that?’ remained as questions. Since I had doubts about the unfamiliar coordinate system called the complex plane, what if we extended this to space? What axis should we add? I thought about such questions.
Looking back at the books that influenced me at the time, I think books like these had an impact. Each series had creative stories using the previous content at the back, and I enjoyed reading those parts.

리만이 들려주는 4차원 기하학 이야기 - 예스24

리만이 들려주는 4차원 기하학 이야기. 우리는 3차원 공간에서 살고 있다. 그럼 4차원은 뭘까? 4차원 공간이 있고 그 곳에서 사는 사람들이나 물체들은 우리와 어떻게 다를까? 이런 의문을 품고 있는 사람이라면 이 책을 읽어볼 것을 추천한다. 4차원 이상의 기하...

https://www.yes24.com/Product/Goods/1483986

Since there was no place to resolve such questions, I sent an email to my math teacher who was my homeroom teacher in my sophomore year.

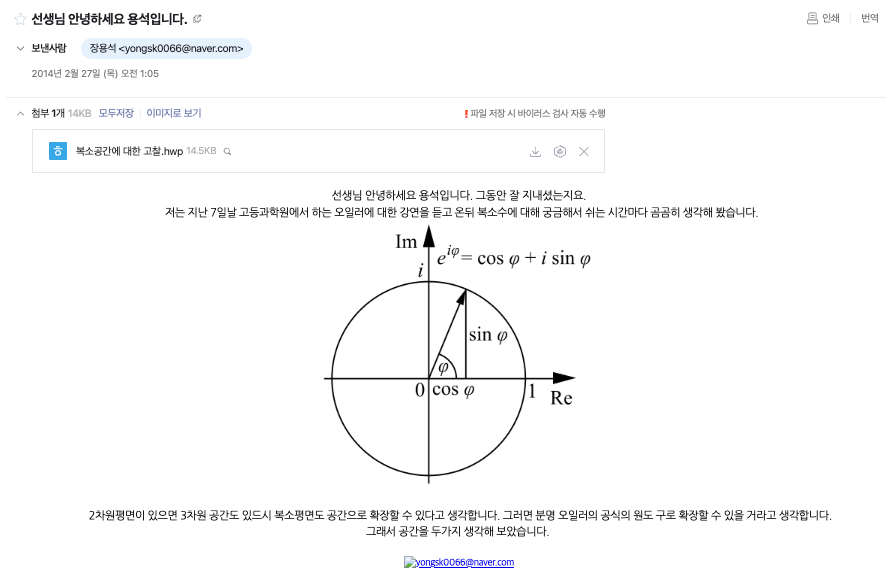
I thought it was quite an innovative idea at the time and sent it, and I received a thoughtful reply.

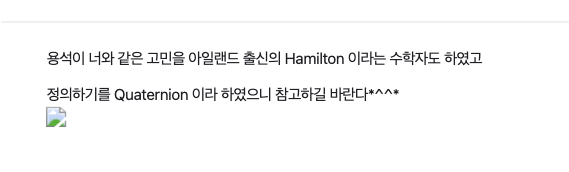
Since it was difficult to find keywords for unknown fields or I lacked the will, keywords were a good answer for me. If I had been more interested in mathematics here, wouldn’t I have dug deeper? After that, I looked up and examined quaternions, but I quickly lost interest because I couldn’t connect what this was for.
More than 10 years have passed, and I suddenly became curious about what answer GPT would have given me at that time, so I asked. This was also the motivation for writing this post.

I often chat with o3 these days, and it’s quite cold and rational. Even considering that, if I had received such an answer at the time, my enthusiasm might have cooled down. To point out such a fatal flaw so precisely. Still, it was a good answer about why quaternions are necessary. I didn’t have the seed of a mathematician, but I think it would have been a great help to someone who needed an answer to a similar question. Perhaps in the future, academic questions will no longer be resolved at school?

It also provided a kind derivation of why j is not a new axis and why we extend from 2 dimensions to 4 dimensions, finally answering my 10-year-old question.

I also picked up keywords about interesting extensions like octonions and sedenions. It would have been really fun if I had spent my school days with GPT. Looking back, that’s what I think.
Anyone who wants to continue the conversation can follow the link below.

ChatGPT - 수학적 한계와 확장

ChatGPT helps you get answers, find inspiration and be more productive. It is free to use and easy to try. Just ask and ChatGPT can help with writing, learning, brainstorming and more.

https://chatgpt.com/share/6805223e-7ef4-8013-90c3-84580538dca3

Coming back, one of my diverging unsolved cases, the question about ellipses, was posted on Facebook.
As mentioned above, since I was fascinated by the properties that orthogonal projection brings, I made mistakes trying to find the perimeter through projection and posted them in a public place. Since there were errors from the beginning, with things being represented as straight lines in the development, I couldn’t prove it myself, but remembering the answers at the time, it was concluded that the perimeter of an ellipse is difficult.

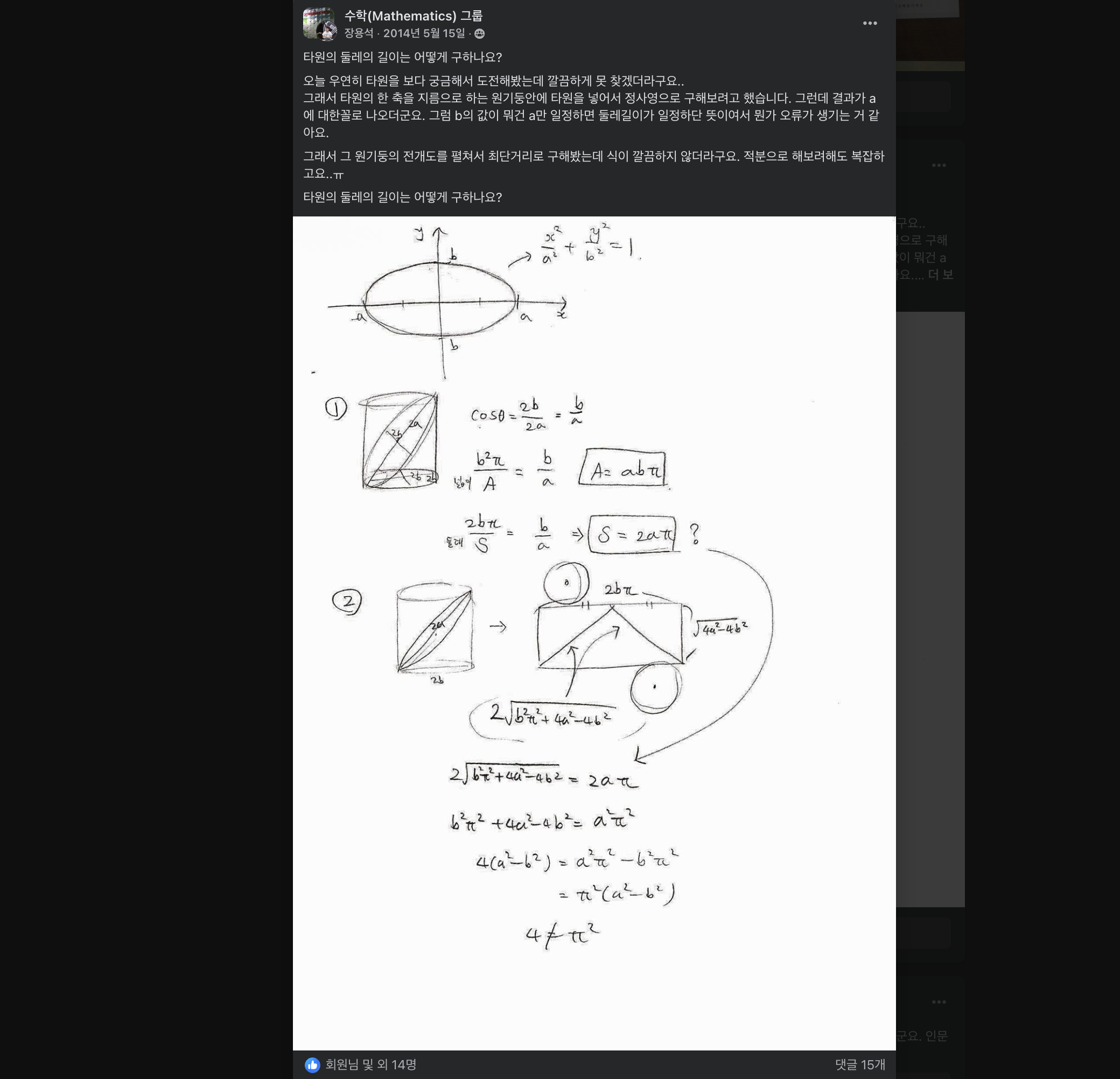
Where did it go wrong?
To fix this question, I first had to check whether the cross-section of a cylinder is an ellipse.
Time passed and although I didn’t graduate from mathematics, with the help of GPT and knowing how to code a little, I made it. Even if it’s not a mathematical proof, I created a simulation to help intuition. Try adjusting various slides and rotating the camera to examine it.

An inclined plane passing through a cylinder. Between them, we put two spheres that are tangent to both the plane and the cylinder, one above and one below.
Let F1 and F2 be the points where spheres S1 and S2 meet the plane, respectively, and let P be an arbitrary point on the intersection of the inclined plane and the cylinder.
At this time, connect P to the tangent points of each sphere in the same direction as the cylinder’s axis, and let these points be P1 and P2, respectively. Even if the position of P changes, the length of P1P2 does not change.

At this time, the tangent lines from point P outside each sphere, PP1 and PF1, PP2 and PF2, have the same length respectively. To understand this more easily, press the View from side button
What is the definition of an ellipse?
It’s the set of points on a plane where the distance from two fixed points is constant.
Since PF1 equals PP1 and PF2 equals PP2, the sum of these two is also equal to P1P2. Then the foci of the ellipse on the inclined plane become F1 and F2.

Dandelin spheres usually are inscribed between a cone and a plane, but in this case, a cylinder works without much problem.

Perimeter of an Ellipse

My big mistake was incorrectly representing the development of the cross-section. It cannot be drawn as a straight line.
To visualize this, I created a cylinder in cylindrical coordinates. It’s similar to before\

Let’s find the equation for height with respect to angle theta (θ) for an arbitrary point P on the ellipse.
Let’s simplify by assuming that the inclined plane has no azimuthal angle and only one inclination angle. The inclination angle α varies according to the plane’s tilt.
When we unfold the cylinder and develop h(θ) on a plane, it’s expressed in the form of a sin function.

At this time, k = r tan α is a constant, so we can see that only the amplitude of the sin function changes according to the inclination angle.
Therefore, the perimeter of the ellipse can be obtained by integrating this function.

In the end, finding the perimeter of an ellipse is equivalent to finding the arc length of a sin function.

When a function y = f(x) is differentiable on the interval [a, b] and the derivative f′(x) is continuous, the arc length L of the curve y = f(x) on this interval is

L = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^{2}} \, dx

Try deriving the formula yourself.
Applying this formula, the perimeter of the ellipse is expressed as follows.

Function : f(θ) = k sin θ (k = r tan α)
Interval : [0, 2π]
Derivative : f′(θ) = k cos θ

Since the interval [0, 2π] has the same shape repeated 4 times, we reduce the interval to [0, π/2] and multiply by 4.

L = 4 \int_{0}^{\pi/2} \sqrt{r^{2} + (k\cos\theta)^{2}} \, d\theta

The $r^{2}$ term here must be included because without it, the perimeter would be overestimated. Expanding k gives us the following form.

L = 4r \int_{0}^{\pi/2} \sqrt{1 + \tan^2 \alpha \cos^2 \theta} \, d\theta

Let’s clean this up a bit.

1 + \tan^2 \alpha \cos^2 \theta = 1 + \tan^2 \alpha(1 - \sin^2 \theta) = 1 + \tan^2 \alpha - \tan^2 \alpha \sin^2 \theta

For convenience, let’s define:

m := \tan^2 \alpha \; (m > 0), \; A := 1 + m = 1 + \tan^2 \alpha = \sec^2 \alpha

Then we can express it as:

\sqrt{1 + m\cos^2 \theta} = \sqrt{A - m\sin^2 \theta} = \sqrt{A} \sqrt{1 - \frac{m}{A}\sin^2 \theta}

Substituting m and A, we can express it as:

\frac{m}{A} = \frac{\tan^2 \alpha}{1 + \tan^2 \alpha} = \sin^2 \alpha

Substituting $\sin \alpha$ with k, we can express it as:

L = 4r \sqrt{A} \int_{0}^{\pi/2} \sqrt{1 - k^2\sin^2 \theta} \, d\theta = 4r \sec \alpha \int_{0}^{\pi/2} \sqrt{1 - k^2\sin^2 \theta} \, d\theta

The integral part is called the complete elliptic integral of the second kind. So we can organize it as follows:

L = 4r \sec \alpha \int_{0}^{\pi/2} \sqrt{1 - k^2\sin^2 \theta} \, d\theta = 4r \sec \alpha \cdot E(k)

Here, E(k) is the complete elliptic integral function of the second kind.

So what does $4r\sec \alpha$ mean here? 4 is the multiplication for each quadrant, and

r\sec \alpha = r \frac{1}{\cos \alpha} = a

corresponds to the semi-major axis of the ellipse. The semi-major axis of an ellipse is commonly expressed as a.
With a little refinement, it can be organized as:

L = 4a \cdot E(k)

Now, even if it’s not a complete proof, we’ve finished the process of deriving the elliptic integral form.

Now let’s calculate the integral. But